Buzz:  Where have I been?

Woody:  Beyond infinity, space ranger.

Buzz:  So where are we now?  

Woody:  In a garbage truck on the way to the dump

Danny emerged from the linhay and looked up at the cloudless sky.  The day was drawing gently to a close.  

“Do you still have some of that whisky, by any chance?”  I did.  I put away the board papers I had been dutifully flicking through, and poured two glasses.  

Natural numbers

Pooh was counting his pots of honey when there came a knock at the door. “14,” said Pooh. “Or was it 15? Bother. That’s muddled me. I just like to know, so I can say to myself: ‘I’ve got 14 pots of honey left.’  Or 15. It’s sort of comforting."

“So you remember what we said about natural numbers?” Danny continued.  “We start with the concept of a single unit.  Then we can conceive of a plurality of those units, all exactly equivalent to each other but having separate identities.  And we can assemble any of those units into a single group, without altering the individual units concerned.  Each of those groups represents one of the natural numbers (ie the positive integers 1,2,3.…, with or without zero as you prefer).  

This leads us to our concept of addition, by which we regard two or more of those groups as being combined into a single group, again without their component units losing their separate identity.  Multiplication is addition repeated, subtraction is addition in reverse, and division is repeated subtraction.  Exponentiation is repeated multiplication or division.  These principles are all in accordance with the generally accepted rules of arithmetic throughout the world.

But these concepts are not inevitable, even when we limit ourselves to the natural numbers.  An alternative concept of addition might involve the units concerned being merged, and losing their separate identity, so that 1+1=1.  Although arithmetic is not empirically founded, its genesis is likely to have been empirically prompted.  So an alternative concept like that could be a natural one in a universe of liquids and gases.  As FCS Schiller observed, if you are counting drops of liquid, it is not correct (or at least may not be correct) that 1+1=2.

1+1=1 would also be correct in this alternative arithmetic.  So 1-1 could equal either 1 or 0.  If I take a small pool from a larger pool I have a small pool left, but if I take the whole of the pool, I have no pools left.  Or you could say that if I take a small pool from a large one I have two pools, so 1-1=2 and 2/2=4.  

You need to look no further than the Christian doctrine of the Trinity to  be reminded that the axioms of arithmetic are constructs and not a priori truths:

‍    Ita Deus Pater, Deus Filius, Deus [et] Spiritus Sanctus. Et tamen non tres dii, sed unus est Deus. 

‍     Alia est enim persona Patris alia Filii, alia Spiritus Sancti: Sed Patris, et Filii, et Spiritus Sancti una est divinitas

On the other hand once we accept the conventional principles, all subsequent correct arithmetic statements derived from them are true analytically, not synthetically, in the sense that 7+5=12 is necessarily correct once you have defined 7,5 and the concept of addition.  12 is simply a synonym for 7+5, and both are synonyms for 1+1+1… If you combine a set of 5 members with a set of 7 members, which is what we do when we add them, the set you get (12 members) is indistinguishable from a set that had 12 members in the first place.  By contrast, even when you have defined the concepts “cat”, “dog” and “chase”, the statement that “the dog chased the cat” is, if true at all, only true contingently, or a posteriori".  

I intervened cautiously.  "But isn’t that the opposite of what Immanuel Kant said about arithmetic?"  "Yes", said Danny, "but he was trying to argue a more general philosophical case against David Hume, so that may have coloured his judgement."

"Once we have chosen our principles, we may make further assumptions that are also expedient rather than inevitable.  We can for example conceive of negative numbers, and the square root of minus one.  Each time we make a new assumption, we can establish an extended set of rules to incorporate it into our system so long as we maintain consistency.

None of this is supposed to be novel or to give a proper proof or explanation of how arithmetic, as we generally understand it, works.  I merely want to summarise what appear to me to be the basic principles of arithmetic, as applied to natural numbers in particular, as a context for talking about infinity”. 

Cardinal infinity

•    “If each of the individual natural numbers can be thought of as a bounded or finite set of elements each of which is an arithmetic unit, then infinity, as a measure of the magnitude, or what mathematicians call the cardinality, of a set, describes a grouping or set of elements that is unbounded in at least one direction and dimension.  So infinity is not a natural number.  But the set of natural numbers provides a simple example of a set of arithmetic terms that is infinite in number of terms.  We can start the natural numbers from a single point (0 or 1, but preferably 1) and then extend the set, one element at a time, in a single dimension (a straight line) and in one direction, moving at each step to the next larger value, which is generated by adding a unit to the preceding value. 

•    Thus the value or label allocated to each natural number tells you both the number of units in that number and the number of natural numbers in the sub-sequence from 1 up to and including the natural number concerned.  These are the cardinal and ordinal aspects of the natural numbers.  They are both intrinsic aspects of the same natural numbers, and result from the way they are generated.

•    We can go on to define the concept of one number being equal to, or bigger or smaller than, another, enabling us to distinguish each natural number from the others.  Otherwise we may end up in a loop, where we say 13 is bigger than 12 because 13 represents 13 units, or the 13th number, and 12 represents 12 units.  We can avoid this circularity by making a 1-1 matching between the units that make up each of the two numbers.  When we do this between 12 and 13, we find that we come to the end of the units in 12 before we come to the end of the units in 13.  So 13 has more units than 12 and so is bigger than 12.  We don’t need to know how many units we matched from each, or how many were left over.  Simply by doing this matching we can rank all our numbers in order of size.  The only other concept we need is that of the single unit, which we already have, contrasted with a plurality of units (ie more than one).  A number which has only a single unit left over after the matching is the next in size, or next in line, while a plurality of left over units (never mind how many) tells you there will be one or more numbers in between the two we were matching.

•    We use a version of this 1-1 matching to establish the number of objects in a finite set.  Imagine a child learning to count with cowrie shells (which happens to be how I was taught).  The child takes successive shells and matches each shell to a natural number taken in their usual order (say 1,2,3).  When the child gets to the last shell, by establishing how many numbers it has used, the child knows how many shells there are.  And the value of the number that matches the last shell, 3, tells the child how many numbers they have used, and thus how many shells there are (3).

•    The magnitude of this set of natural numbers as a whole, meaning the number of terms in the set, is what I mean by “infinity”.  And any other set of arithmetical terms that we can show is equal in number of terms to that set will be of the same magnitude, or equinumerous - that is, those terms will also be infinite in number.  On the other hand any set that we can show has a larger number of terms than infinity, ie is supernumerous to it, will mean we have found a number larger than infinity.  When I refer to an "unbounded" or "unlimited" set of elements, I mean one that may be either equinumerous with or supernumerous to infinity.  This concept of infinity is the inevitable consequence of our concept of the natural numbers, since there cannot be a last number in the sequence as we have defined it.

•    If we then take a second set, consisting of the same natural numbers but adding -1 as a single additional term, are the two sets equinumerous?  They don’t look the same, as each term in the first set has a corresponding term in the second, while the second set has one term, -1, that does not appear in the first.  

•    But consider this: both sets are unbounded in one dimension and direction, so we can start at the beginning of each and match each element in the first with an element in the second, so that no member of either is unmatched.  Or if you prefer, we can change the second set into the first by adding 1 to each element of the second.  They are then indistinguishable.  Similarly, if you think of the numerical values as labels, you can remove the labels from the elements of each set, so that all the elements look the same, and the sets are then identical.

•    Our changes cannot have changed the number of elements.  This is because each natural number represents a single element in the set of natural numbers, irrespective of its value.  So increasing or decreasing its value is like changing the number on a pool ball; it is still a single ball.  Similarly if you remove the label entirely.  However when we consider an individual natural number as a set of units, so that 7 is a set of 7 units, then adding or subtracting units  to or from that set changes the number of elements in the set.  If I add 3 to 7, I have taken my set of 7 units and added to it a set of 3 units, producing a set of 10 units".

I mean what I say

"When I use a word," Humpty Dumpty said, in rather a scornful tone, "it means just what I choose it to mean—neither more nor less".

"Could you just remind me what some of these expressions mean?" I asked.  

"Of course" Danny replied.

•    "By set I mean a grouping of numbers or other things that are equivalent to each other for the specified purpose of the grouping but also distinct from each other; a set may also contain a single thing or be empty.  I don’t mean a set as defined by any particular set theory in mathematical logic.

•    The things contained by a set are its members,  Those members may in turn be subsets of the main set.  

•    Members which are not themselves subsets in a particular context I also call elements, and I sometimes refer to elements which are numbers as terms. 

•    Sequence means a set of numerical values or other elements ordered, either randomly or not, in a single dimension such that you can identify every element in the set and its place relative to every other element, and series means a sequence ordered non-randomly according to a rule."

Infinity in different directions

Danny paused.  “Do we have some crisps? I don’t think I had any lunch.”  I provided a bag.  Danny tore, crunched and resumed.  

•    “So for the reasons I have just explained, infinity + i = infinity, where i is any positive integer. 

•    Similarly, if we take two infinite sets, such as the positive and the negative integers, we have infinity in one dimension but two directions.  But we can take one element from each set alternately, each time matching the element we take to the next larger natural number.  So we can say infinity + infinity = infinity.

•    And as multiplication is repeated addition, infinity*i = infinity, by a process you might call infinite ascent (I believe mathematicians call it proof by induction); infinity*2 is infinity, so infinity*3 is infinity+infinity+infinity, = infinity*2 + infinity, = infinity + infinity, = infinity, and so on.   Indeed as we can repeat this process without end, we can say infinity*infinity=infinity^2=infinity.  We can visualise infinity^2 as infinity in two dimensions, like a grid based on the Cartesian plane with sequences of points extending without limit in the space bounded by the positive x and y axes.

•    We have a simple way to check that infinity*i = infinity. Take a page of a spreadsheet and write all the natural numbers on it, in base 10, from 0 onwards in a single column.  On a second page, write the identical numbers on it 10 times, in 10 identical columns.  Each number on the first page now appears 10 times on the second page; page 1 contains one infinite set and page 2 contains 10 identical infinite sets.  And yet each page contains the same number of numbers in total.  To show this, take the first column on page 2, and write a 0 at the end of every number.  Put a 1 at the end of every number in column 2, and so on.  We haven’t changed the number of numbers on page 2, just their digits, yet each number on page 1 now appears once only on page 2 and we have a 1-1 matching between the two pages.

•    Continuing our infinite ascent, infinity^i = infinity, and infinity^infinity = infinity.  And as an extension of our image of the Cartesian plane, we can also conceive of infinity^infinity as a hypercube of points extending without limit from a single origin in an infinite number of dimensions.

•    By the same means (infinity^infinity)^infinity = infinity, and so on.  The Jain mathematicians of India referred to infinity in up to 5 directions or dimensions, time being the fifth - we are just taking that a bit further.

•    i^infinity must also be equal to infinity.  2^infinity is 2*2*2.… which is 2+4+8+16…, which converts readily into (1+1) + (1+1+1+1)… , which has to be equal to infinity - it’s infinity in one direction.  And the same approach applies where i is any larger integer than 2.

•    That still leaves fractions and other sub-divisions of the gaps between integers, which we’ll come to a bit later".

Bijection and sequencing - general

•    "First, we need to pin down the principles we’ve just summarised.  Mathematicians require that to prove an unbounded set is equinumerous with the natural numbers, and thus has an infinity of members (and no greater number), the general principles I’ve just summarised aren’t enough.  We must prove specifically that there is a bijection, or 1 to 1 matching, from (i) each member of the set whose terms we wish to count to (ii) a unique element of the set of natural numbers, and vice versa.  (The vice versa is less important - it just confirms that the set you are counting isn’t smaller than the set of the natural numbers).  In each direction no element in the set you start from can be omitted, and every such element must be the only element to match to its target element in the other set.  This approach reflects the fundamental way we compare the size of two numbers that I described earlier.  It was I believe first stated by the same David Hume I mentioned before and is known as Hume’s Principle: 

‍     "When two numbers are so combined, as that the one has always a unit answering to every unit of the other, we pronounce them equal"

•    Because our sets each have an unlimited number of members, to do the matching we have to be able to put each set into some sort of sequencing, by magnitude or otherwise, which enables us to identify the position of each member in that sequencing and be sure we haven’t missed any out.  You might think that even if you can’t do this for a particular unlimited class of numbers such as the transcendental numbers (I’ll try to explain what they are in a minute), you could achieve the same result by randomly picking terms from that class to match 1 to 1 with the natural numbers.  Because you have an infinite number of natural numbers to match against, and each transcendental number once matched can be disregarded thereafter (ie the socks are not put back in the drawer), if you carry on long enough, then any given transcendental number is surely bound to be picked and matched with a natural number through this process.  But that isn’t true.  

•    You could pick transcendental numbers for all eternity and if your process is genuinely random your chances of picking any given transcendental number at some point in the process will always be zero - definitely not 100%, which is the probability we need and which would be provided by a complete 1-1 matching.  In a finite set of numbers with n terms, your odds of picking a particular term at random with one pick are 1/n. As n increases your odds get smaller, tending towards zero.  While they will never reach zero for any finitely large value of n, if n is infinite the odds must always be shorter than they are for any finite value of n (as infinity is bigger than any given integer), so they can only be zero.  And no matter how many you pick, if you pick them singly you always have infinity left. 

•    The converse of this approach is equally true.  If you can establish a 1-1 matching of this kind between two numbers, or sets of units, they have to be equal - you cannot say one is bigger than the other.

•    The accepted way to demonstrate this matching in the 19th century was to put the elements of the set whose elements you wanted to count into a single sequence that you could show included every element of that set.  This sequence can then be matched 1 to 1 with the natural numbers, which as we have seen can also readily be put into a single sequence.  This was the version of bijection used by the 19th century German mathematician and theologian Cantor.  And certainly if you can arrange the elements of a set in this way as a single sequence, it is straightforward to match them with the natural numbers.  But as we shall see, you can’t always do it with with unbounded sets of numbers each of which numbers is unbounded in its expression and where there is no least or minimum interval between the numbers.  In particular, you can never find the next number in magnitude to any such number - indeed you cannot fully express the number at all in the case of many of the transcendental numbers.  

•    For example you cannot sequence the rational numbers (ie fractions) between 0 and 1 by size, nor the algebraic numbers (roughly speaking, numbers which can be specified by an algebraic equation with rational coefficients).  Take the interval between 0 and 1.  You have an infinite number of fractions in that interval in the form a/b where a< b and both are positive integers.  Make sure you have reduced the fractions and removed any duplicates.  Now take any two of those fractions, as close together as you wish.  They must be different in size as they are different numbers - call that difference g.  You can now take the fractions (a/b)*g using every a/b fraction in the interval between 0 and 1.  So between every pair of different rational numbers there will be exactly the same unbounded number of rational numbers as there is between 0 and 1, or between any other pair of integers.  It’s like a fractal in this respect.  The same is true for the algebraic numbers.

•    Cantor proved that although you cannot sequence rational or algebraic numbers by the size of the numbers, you can do so by the size of their component elements, (ie their numerators and denominators).  These are expressible as integers and thus the intervals between them are not infinitely sub-divisible, and in addition the number of those component elements for each rational or algebraic number is finite.  For example the rational numbers can be sequenced ½ ⅓ ⅔ ¼ ¾ etc (excluding reducible fractions to avoid duplication).  You will see how to sequence rational numbers and irrational algebraic numbers in this way in Wikipedia.  

•    This also illustrates an important point: two sets are equinumerous so long as at least one arrangement can be found that enables you to establish a bijection between them, even if you can’t do this with other arrangements.  This is not an arbitrary axiom we can adopt or not as we prefer.  Changing the arrangement of units in a set cannot change the number of those units.  Set A cannot be bigger than set B in one arrangement but the same size in a different arrangement.  If Set A can be bijected with Set B in at least one arrangement, the fact that you can’t biject them in a different arrangement can only mean that it is the way you have arranged the members of one of the sets that causes this, not the number or quantity of members in that set

‍ •    But some real numbers, the transcendental numbers, can’t be sequenced either by size or by any other characteristics or components without missing out one or more elements.  So, it was said, there could be no 1 to 1 matching with the natural numbers.  So the number of terms in such a set, whose terms could not be sequenced, was "uncountable".  Cantor said as long as it was not provably smaller than or equal to the set of natural numbers, arranged as a single sequence, such a set must be supernumerous to the set of the natural numbers, that is to say larger in number of elements than infinity.  This would apply to any set of numbers that Cantor could show must always have one or more elements outside any given unbounded sequence of those numbers.  

•    The problem with this is that the reason why a set of numbers can’t be sequenced into a single sequence isn’t necessarily that it has more elements than the natural numbers.  It may just be a result of the form of the numbers.  You can’t assume a set whose members cannot be put into a single sequence of any kind is necessarily bigger, in the cardinal sense of containing more elements, than one which can be so sequenced.  Here are three situations where this is not the case. 

•    First, we might have a set of numbers we cannot put in a single sequence, but we might be able to divide that set into two or more unbounded subsets each of which can be separately sequenced and matched 1 to 1 to a different sub-sequence of the natural numbers.  For example if we have a set consisting of two unbounded sequences A and B, we can divide the natural numbers into the odd and even integers. Then if we can biject sequence A with the set of odd numbers and sequence B with the set of even numbers, we have achieved an exact bijection of every element of our set with the set of the natural numbers and neither of those sets can be bigger than the other.  I’ll call this multi-sequence bijection.  

•    Secondly, even if you have a set you can’t biject with the natural numbers in two or more subsets as just described, if this "uncountable" set is in the form of a set of sets, you may still be able to biject the individual elements of all the subsets with the natural numbers.  This seems counter intuitive, since if anything the number of elements should be greater than the number of subsets, assuming each subset has a plurality of elements, but it arises because it’s the form of the members of the set that stops you bijecting the members themselves, not the number of them.  I’ll call this indirect bijection.  

•    Thirdly, you may be able to show a 1-1 correspondence between two or more sets without sequencing or counting either of them, simply by reference to the way the sets are each constructed.   I shall refer to this as bijection by construction".

Danny paused for refreshment.  "This reminds me of the story of the three wise men and the angel.  

A mathematician and a philosopher wanted to establish once and for all how many angels could dance on a pinhead.  So they stuck a pin in a wine cork and enlisted the services of the heavenly host.  

'I might be able to work this out from first principles', said the philosopher.  'But it could take time.  I’ll need to read all the great philosophers and theologians of the past to see if they say anything relevant.'

'I’ve got a better idea' said the mathematician.  'I’ll count them.  I’ll just need them to stand in a row, so I can be sure I include them all'.  

'That won’t work' replied the philosopher.  'If you put them all in a single row they won’t fit.  You’ll have to put them in lots of rows.  Then you’ll need to stop them moving around.  Look at them - all scurrying about like ants.'

At this point there was a cough.  A small mutinous face looked up at them from the pin.  'We’re angels.  We do praising, and descending from on high.  We can throw in a few hosannas.  But we don’t do standing to attention in rows.  You want the Grenadier Guards for that.’  There was a silence.  

Then a scientist, who had been listening to the discussion with interest, intervened.  ’If you want to get them standing still in rows, wait till 6 o’clock,' she said.  'Why, what happens then?' asked the mathematician.  'They’re angels' she replied.  'That’s when they have choir practice'."

Single sequence bijection

"So next I’ll describe some sets of numbers which are not presented as single sequences but which we can put into single sequences and thus biject with the natural numbers in the traditional way.  The simplest and surest method is to convert some or all of the elements of the set by one or more formulae into new numbers and show that the resulting set is the set of natural numbers; but it is not the only method.   

All the elements of the sets are integers at this stage.  Integers are finite in their expression and there is a minimum interval between them, which is 1.  This means we can concentrate on the number of elements (ie individual integers) in each set for now, without the complications of sets whose elements are infinite in their expression and have no least or minimum interval between those elements.  

•   infinity+i: take all the positive integers, and the negative integers from -1 to -(i-1).  Add i to each element and you get the natural numbers.

•    infinity+infinity: take the positive and negative integers.  Multiply the negative integers by -2, and multiply the positive integers by 2 and subtract 1.  This gives you the natural numbers. 

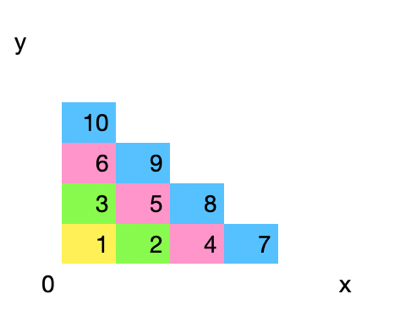
•    infinity*i: divide the positive integers into subsets the first of which is all integers that are 0 base i, then all that are 1 base i, and so on up to i-1 base i.  Each subset will be infinite and there will be i subsets.  All the elements will be unique.  This is the same as taking an x,y two dimensional plane of Cartesian co-ordinates and then building i sets along the x axis where each set extends to infinity along the y axis. You build the sets by taking successive sweeps across each of the i sets adding the next higher natural number each time".  Danny showed me a diagram.

•    "infinity*infinity: no number can be expressed in base infinity, as no number can be divided by infinity to give an integer value with either no remainder or an integer remainder.  Instead, we can make a grid based on the Cartesian plane consisting of an infinite number of infinite sequences, each sequence being a single dimension and single direction, as it was in infinity*i.  So the set as a whole is unbounded in two dimensions and two directions.  We can’t make horizontal sweeps, as they would be endless, so instead we make diagonal sweeps consisting of successive natural numbers, starting at 0,0 then moving +1 along the x and y axes for each sweep, and including the values on the diagonal between them.  As before we allocate successive natural numbers to each of those successive co-ordinates.  We never get to the end of the sequences in either direction.  But as with the unbounded sequence of natural numbers, each element of these unbounded sequences has a finite location in the grid identifiable by its unique x,y co-ordinates, so every such element can be located and allocated a unique natural number.

•    This process creates at x=1 the infinite sequence of triangular numbers 1,3,6,10….and then each successive value of x begins a sequence starting at n-(x-1), where n is each of the successive values of the sequence for x=1.  The first gap (between the first and second terms) for the sequence from x=2 is then equal in size to the second gap for x=1, and so on.  Thus we have apportioned the positive integers into infinity*infinity different elements, capturing each element with a separate and identifiable natural number."  Another diagram from Danny made this clear..

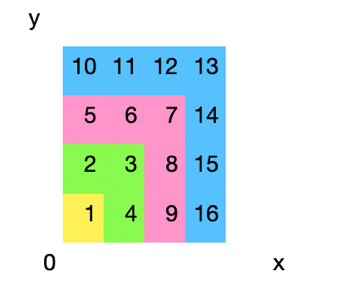
•    "In fact, although diagonal sweeps are conventional, for reasons I’ll come to, it is more convenient to take successive squares.  We start at 0,0 as before, then allocate natural numbers to the co-ordinates 0,1  1,0 and 1,1.  Then 0,2  1,2  2,2  2,1  2,0.  And so on.  Each layer we add comprises of d natural numbers where d is the difference between the two squares of adjoining natural numbers concerned.  eg d=1 is 1^2-0^2, d=3 is 2^2-1^2, d=5 is 3^2-2^2 etc".  And another diagram. 

•   " i^infinity: this is just i*i*i*i…., which is infinity in one dimension and direction.  For any value of i, it is the sum of i^1+(i^1*(i-1)) + (i^2*(i-1))….which can be expressed as a series of additions of finite integers, which in turn can be expressed as 1+1+1…. and so precisely corresponds to the number of natural numbers.

•    infinity^i: all we have to do is use the same set as for infinity*infinity but substituting the positive primes for the natural numbers.  As shown by Euclid, the series of positive primes has no end.  And because they are primes we can multiply every value in any sequence x=n by every value in each and every other sequence x=n(2), n(3) etc, up to x=i, and create a different integer each time (as multiplying different prime factors always results in different products by the fundamental theorem of arithmetic).  So if we take all the different combinations of the elements of {x=1} * {x=2} * {x=3}… for all values of x to x=i, we have infinity^i possible combinations and values.  As each of those values is a different positive integer we have created a set of infinity^i different positive integers.  (I use {set A}*{set B} to mean I take each member of set A and multiply it by each member of set B).

•    Another way of bijecting infinity^i is to take the successive squares we used for infinity*infinity, which of course is infinity^2, and extend our x,y Cartesian plane to i dimensions.  We then allocate our natural numbers to each number in the difference between successive cubes of those natural numbers for i=3; tesseracts for i=4, and hypercubes for each greater value of i thereafter.

•    We cannot use the same procedure of multiplying primes for infinity^infinity as we used for infinity^i, as we would then have values equal to the product of an infinite number of factors.  Even though the individual factors may all be different, the product of an infinite number of any integer factors each greater than 1 is always infinity, so every value they produce is also infinity; we get no natural numbers and all the terms we generate are the same.  

•    One way round this is to use the infinity^i two dimensional grid of primes for x=1 towards x=infinity, but then to put a fractional separator (ie in base 10, a decimal point) in front of the product.  Then we get a set of numbers which although infinite in their expression are each unique in magnitude.  They will often be transcendental numbers.  You will not be able to write down any part of one of these numbers, as all its digits will be subject to change each time you multiply the previous total by the next prime.  But you will be able to define it as the product of a unique infinite series of primes, the value of which is unique at every step in each series (as unique prime factors when multiplied give a unique product) and you will have infinity^infinity such unique series.  So long as I can biject the transcendental numbers with the natural numbers (which I’ll come to later) I can therefore biject infinity^infinity values with an infinite set (ie the transcendentals).  

•    Or a simpler way is to use another version of our hypercubes.  I am not sure whether we could have a hypercube of infinite dimensions, but what we can do is start with the single point 0,0, then extend to the square of co-ordinates 0,1  1,0  1,1 and thence to the cube 2,2,2 etc; moving 1 point along each axis at each stage and adding an additional axis, or dimension, at each stage, and then backfilling to include all the co-ordinates not captured in the previous stages.  The number of natural numbers to add at each stage follows the sequence 1,3,23,229…and is given by n^n-((n-1)^(n-1)) where n is the number of axes at each stage.  You never get to the end, but that’s always true of bijection of members of infinite sets.  What you can do is specify exactly what natural number matches any given n-cube co-ordinate, and vice versa.  Not a hypercube of infinite dimensions, but a succession of hypercubes each having a finite number of dimensions greater by 1 than the previous one, without limit.  

•    And once you have infinity^infinity, you can readily move on to infinity^infinity^infinity… In our hypercube, each infinite subset of natural numbers in a single direction and dimension (eg the (x=1) series) can be expanded into a new hypercube, or we can form the hypercube out of primes instead of natural numbers and then multiply together all the elements of two or more subsets.  And you can exponentiate the primes.  After that, if you want to see a more extended range of transfinite values, all of which are recognised by mathematicians as still being cardinally equal to infinity, ie countable, look at the multiples of ω and ε you will find in descriptions of transfinite ordinals.  The principles are identical".  

‍ Other kinds of bijection

"So far we have been converting multiple sets into single sets and sequences, to match them 1-1 with the natural numbers in their own standard sequence, arranged according to their size.  Let’s see how the other kinds of bijection work in a bit more detail.

•    The most obvious case is where we reverse the process I’ve just described, by multi-sequence bijection.  We can separate the natural numbers into any finite number of infinite sequences by writing them in any integer base i and then taking the sequences from 0 mod i to (i-1) mod i.  In fact for every example in the previous discussion where we combine multiple sequences into a single sequence, it must be the case that we can take a single sequence such as the natural numbers and divide it into the corresponding multiple sequences.  It will then always be possible to biject any such group of infinite sequences of the natural numbers with an equal number of other infinite sequences.  Just as the infinite sets of the natural numbers together add up to infinity, so also must the sequences that we have bijected with them. 

For example if I have three infinite sets of dogs, cats and mice respectively, it may for obvious reasons be undesirable to put them into a single set or sequence, even though I can sequence each animal family separately.  But I can still biject them with the natural numbers by dividing those natural numbers into three separate sequences comprising the 0 mod 3 numbers, the 1 mod 3 numbers and the 2 mod 3 numbers, and bijecting one family with each sequence. 

This process is equivalent to the way mathematicians count ordinal numbers, as we will see.  It is important to understand that this is not a question of choosing to adopt, or not adopt, multi-sequence bijection as one of our fundamental principles; it is inherent in our concepts both of bijection and of the natural numbers themselves.

•    Next, I may have two separate sequences.  I biject sequence A with the natural numbers N and I biject sequence B with the natural numbers N.  I may be unable to biject A directly with B for some reason - perhaps they are cats and dogs again.  But if A=N and B=N, where N is the number of elements of the set of natural numbers, I am entitled to infer that A=B.  Similarly, if A=N and A=B, we can infer that B=N even if we can’t biject B and N directly.  I called this indirect bijection.

•    Lastly (though you may come up with other examples of your own), consider the following situation.  There is a very large hotel run by an eccentric German mathematician, called the Grand Hotel.  It goes on for ever and has an unbounded number of rooms.  It has a possibly unbounded number of guests in residence in some but not necessarily all of the rooms, one guest per occupied room.  Each occupied room has a single key.  All the guests go out for the day, and they all leave their keys at reception, since an alarm goes off if they leave with the key in their pocket.  The hotel manager has no idea how many rooms have guests.  So the receptionist points out that the number of keys left at reception must be equal to the number of guests, even if you haven’t counted or sequenced either the occupied rooms, the guests or the keys, or tried to match any of them up 1-1.  This is because the set of room keys has been constructed so that it has to match the set of guests 1-1.  This is what I called bijection by construction".

I caught the coat tail of an idea as it floated by during this explanation.  "But I read somewhere that the number of real numbers in binary and the number of members in the power set of the natural numbers are both cardinally bigger than infinity, but also both equal to 2^infinity.  Doesn’t that mean there is something wrong with your bijections?"

Danny seemed pleased.  "You are referring of course to Cantor’s proofs that the number of real numbers is greater than the number of the algebraic numbers, and that the number of elements in the power set of the natural numbers is greater than the number of those natural numbers."

The problem with i^infinity

•    “Cantor proved that transcendental numbers, which are a subset of the real numbers, exist, and he also provided a way of constructing some of them.  Through that proof and by a second, similar, proof he established that the number of real numbers is uncountably greater than the number of the rational and algebraic numbers.  And he proved that the number of elements in the power set of the natural numbers is greater that the number of natural numbers.  While western mathematicians have reservations about some aspects of these proofs individually, the main result, which is the existence of a series of super infinities (ie numbers supernumerous to infinity) of ascending magnitude, is accepted as a central component of western mathematics.

•    For any base i in which the real numbers are expressed, the number of real numbers is i^infinity, since the real numbers can be regarded, as I’ll explain later, as every possible infinite sequence of digits expressed in any integer base including a fractional separator.  So there are i possible options for each digit of each number, meaning that the total of the possible numbers is i^infinity.  The result is that if Cantor is right, and if it is correct that there are i^infinity real numbers, i^infinity would have to be supernumerous to infinity, which we have just demonstrated is not the case.  So this is an anomaly.

•    The power set of the natural numbers consists of subsets containing every possible combination of natural numbers ranging from a single digit to all possible infinite sequences of digits, plus the empty set.  You might think this gives infinity^infinity permutations, but in fact the subsets are not sensitive to the position of the natural numbers in the sequence; {1,2,3} is the same subset as {3,2,1}.  This is the normal principle that applies to the members of a set.  So in any subset a given natural number is either in or out, with the result that there are 2^infinity possible permutations, the same as for the real numbers in base 2.  Cantor’s proof that this power set is supernumerous to the natural numbers is different from his proofs in relation to the real numbers, but again it has the result that the number of subsets in the power set, ie 2^infinity, must be greater than the number of natural numbers.

•    Many amateur mathematicians have claimed to  be able to disprove one or more of these proofs entirely.  So far as I know most such attempts are of the "so bad it’s not even wrong" variety.  However Cantor’s proofs, as we shall see, are all incorrect to the extent they are alleged to prove the existence of one or more cardinal super infinities.  They do prove other things, such as the fact that transcendental numbers cannot be sequenced into a single sequence, or that the real numbers must include transcendental numbers.  But there is no valid proof in Cantor’s work of the existence of cardinal numbers greater than infinity, and nothing in what I have encountered in western mathematics that proves their existence".

Real numbers: preliminary   

•    "Transcendental numbers are infinite in their expression and do not have a definable rational or algebraic formula.  This suggests that you can never precisely specify them numerically, although you can approximate them more and more closely.  Like pi.  The same seems to be true of the irrational algebraics like √2.  They are different in this respect from recurring fractions in positional notation (eg decimal fractions, in the case of base 10), or infinite bounded sequences such as ½ + ¼ +⅛ ….which tend to a target (in this case 1), never reach that target at any particular step, as each step adds half the remaining gap without end, yet in infinity do reach that target.  ½ + ¼ +⅛….extended to infinity is exactly 1, not nearly 1.  Despite Zeno’s mischief, there is a simple proof of this; his paradox might be better called Zeno’s fallacy.  Similarly 0.3 recurring is exactly one third, as can be readily proved.

•    It seems likely that each approximation of either an irrational algebraic number or a transcendental number, extended into infinity, is unique to a single such number, and vice versa.  And Cantor when discussing transcendental numbers used for convenience the set of every possible infinitely extended digital sequence in positional notation between 0 and 1 (IEDS).  So I will make the assumption that the transcendental and irrational algebraic numbers in this form consist of every possible variation of non-recurring IEDS.  We can look at those between 0 and 1, since adding the corresponding fractions between every other pair of adjoining integers does not increase their total number, nor does the use of a smaller interval reduce it.  You can see this by considering all the possible different IEDSs between 0 and 1, and then starting each sequence with a rational digital sequence lying between 0 and 1, eg 0.123456789.  The number of different available sequences is the same.

•    If the IEDS for a transcendental number (or at least a transcendental number that like pi has an irrational definition), or for an irrational algebraic number, never exactly equals the number concerned even at infinity, then as well as the IEDS itself you might think we ought to count the corresponding number, which is not an IEDS, as a different real number.  But if we were to do so, it would makes no difference to our analysis.  If we find that the set of all IEDSs is countable, the set of the corresponding irrationals must be countable as well.  

•    It can be shown that between both any pair of rational numbers and any pair of transcendental numbers expressed as IEDSs (or for that matter a pair consisting of one of each) there is an unlimited number of rationals equinumerous with the set of all rationals, and an unlimited number of real numbers (ie including the transcendentals) equinumerous with the set of all real numbers, in each case irrespective of the number of all rational numbers and the number of all reals. Danny handed me some notes. 

•    We know that the number of rational and algebraic numbers is in each case infinity (and not greater) as they can each be arranged, with no possible omissions, in a linear sequence corresponding to the natural numbers.  So after some minor adjustments I’ll come to later, if the number of IEDSs is greater than infinity, the number of real numbers, and thus the number of transcendental numbers, must also be greater than infinity.  But if not, not".  The glass was extended.  I poured.

Cantor’s first real numbers proof

•    "Cantor published his first proof in 1874, along with his proof of the countability of the algebraic numbers.  I won’t summarise all of the proof here, as it also involves his proof of the existence of transcendental numbers, but you can find an outline in Wikipedia.  The relevant part of it goes something like this:

‍    (i)    For the base case, take the sequence of algebraic numbers between 0 and 1 ("algebraic" includes rational numbers but here and elsewhere refers only to real algebraic numbers).  Pick the first two in sequence.  Then pick the next two in the sequence that lie inside the first two in terms of their magnitude, ie that are smaller than the bigger of the first two and bigger than the smaller of them.  Keep dong this to create an infinite sequence of nested pairs each sitting wholly between every previous pair.  It is easier to see how this works if you take the conventional sequence of the rational numbers; Wikipedia shows you this sequence.  The principle is the same in both cases.

‍    (ii)    This sequence will converge, in the case of the rationals and the algebraics, on a single target number in every case, and that target number must always lie within every pair of numbers in the sequence as otherwise the sequence wouldn’t be infinite.  So it also follows that the target number can’t be a number in the sequence.  As the sequence of rationals contains all the rationals, the target for that sequence won’t be a rational; for example in the case of the sequence of the rationals between 0 and 1, it’s (√2)-1.  And with the algebraics the target cannot be a rational or an algebraic, assuming algebraics include rationals - and it isn’t.  It has to be something else which is a real number but not a member of the sequence, so it is a transcendental number.  

‍    (iii)    Although Cantor extends his proof to sequences that converge on two separate target numbers for completeness, all the sequences we are concerned with contain all the rationals and algebraics.  And as we have already shown, there is an unbounded number of rationals and algebraics between any two real numbers, so the sequences can never converge on two separate numbers.  Incidentally, this is probably a blessing for Cantor, since one of the limbs of his proof in the case of two target numbers covers the situation where the number of items in the sequence is finite.  So he appears to be arguing that a finite sequence plus a singleton transcendental that is outside that sequence is not merely equal, but supernumerous, to infinity. 

‍    (iv)    You can continue this process to apply it to your new set consisting of the algebraics plus the single transcendental you generated, and to apply it to any subsequent set so generated.  You can also put the numbers in your sequence into a different order, so long as they are still all in a countable sequence, and of course you can choose different starting intervals.  The proof applies to any sequenceable set of real numbers, though to make sure you generate a transcendental you must always include all the rationals and algebraics in your sequence.  You cannot however extend the process to generate a set of numbers beyond the transcendentals, because the transcendentals as a whole can’t be sequenced, as we shall see.

‍    (v)    So this means there will always be a number lying beyond any reducing sequence of pairs of algebraics which can only be a transcendental.  Initially, I believe that Cantor’s main interest in his proof was that it both demonstrated the existence of transcendental numbers and provided a way of generating them.  Only later on did it occur to him that it also appeared to show that there were more real numbers than natural numbers; the reason being that as the target is always beyond the sequence, you can never construct a sequence including both the target and the sequence with which you started without thereby also generating a new transcendental number beyond the combined sequence.  Cantor believed that you have to sequence the members of a set into a single sequence to biject that set with the natural numbers, so this extra number meant you could never achieve this bijection and the reals must be supernumerous to the natural numbers.

‍    (vi)    There is an unbounded number of sequences of this kind that you can construct, so the number of transcendental numbers lying outside any sequence you create of the rational and algebraic numbers must also be unbounded; although a single such transcendental is sufficient, based on Cantor’s analysis. 

•    This proof has a simple problem.  Cantor thought that because there would always be a transcendental number outside his sequence of algebraics, it was impossible to biject even a single such sequence, plus its generated transcendental number, with the natural numbers, so even a single such sequence plus the transcendental must be supernumerous to the natural numbers.  But an infinite countable set, plus a separate singleton set, is our most basic example of multi-sequence bijection.  

•    Next, changing the starting interval for the sequence increases the number of transcendentals so generated.  If you take all starting intervals defined by rational and / or algebraic numbers you get infinity*infinity intervals, each of which can be assumed to generate a different transcendental.  But infinity*infinity is unbounded but still countable, ie equal to infinity.  

•    Changing the order of the items in a sequence potentially generates a different transcendental from that generated by the same original interval.  In the Wikipedia rational sequence we could for example decide to take ⅔ before rather than after ⅓.  But the same result can be achieved by changing the starting interval rather than the sequence thereafter, so no additional transcendentals are generated. 

•    Adding transcendentals to the sequences or to the endpoints of the starting intervals may generate further transcendentals, but to determine whether the number of transcendentals so generated becomes greater than infinity you need to know how many transcendentals there are.  So at best the exercise is circular and you still have to find another way of determining the number of transcendentals.  In fact, since each such additional transcendental has to be generated from a previously generated sequence, the set of transcendentals so generated (which of course may not be the full set of transcendentals) is sequential and so capable of bijection with the natural numbers and thus countable.

•    A few years later, Cantor published a revised version of this proof referred to as the "everywhere dense" proof.  But that was also based on proving the existence of an intersection of a different kind of series of pairs of rational / algebraic numbers, so the problem with the proof is the same.

•    Cantor doesn’t claim that his proof constructs every possible transcendental number.  So while we have shown that the transcendentals he generates with his proof are countable, or at least not proven to be supernumerous to the natural numbers, we still need to consider whether we can determine the number of transcendentals as a whole.  First, let’s look at Cantor’s other, more famous real numbers proof."

Cantor’s second real numbers proof, or the diagonal proof

•    "Cantor tried again a bit later, with his famous diagonal proof.  Again you can read about this in Wikipedia.  It is beautifully simple.  Cantor said whatever infinite sequence you create consisting of real numbers, you can always specify a number that is also a real number but is outside that sequence.  

•    Cantor took the set of all IEDSs between 0 and 1, expressed in base 2.  It’s a simple set to define.  There are some cases where two different IEDSs are equal to the same decimal fraction.  This occurs whenever the sequence ends in a 0 followed by 1 recurring, which is equal to the number you get if you replace that 0 by a 1.  So 0.00<1 recurring> is the same as 0.01, just as 0.1<9 recurring> is 0.2 in base 10.  Once you’ve adjusted for duplicates like that you can then express all real numbers, including non-recurring rational numbers, as a unique IEDS, because you can include recurring zeros.  

•    Cantor invites you to create any unlimited sequence you want of these IEDSs (the target sequence).  Then he creates one or more infinite sequences of digits each of which is different from the first element in the target sequence as to its first digit, and so on for every successive digit.  In base 10 he would have a choice of 9 digits for each relevant position in his new numbers, giving him 9^infinity numbers outside the target sequence.  In any base i the number of possible digits at each relevant point for Cantor’s numbers is i-1.  In binary, which is the base Cantor used, there is only one number outside the target sequence created by his process, but he says that is enough since it cannot be in the target sequence and so (according to him) cannot be included in any bijection of the natural numbers with that target sequence.  By "bijection" he again meant single sequence bijection only.

•    I will call these numbers outside the target sequence that are created by Cantor’s procedure C numbers, and I will call the target sequence and its associated C numbers together a diagonal set.  

•    Cantor says that he has proved the IEDSs can never be put into a sequence that includes all of them, because there will always be at least one C number left out.  So the number of IEDSs cannot be bijected with any infinite sequence such as the natural numbers, and thus must be greater than the number of elements in any such sequence, and so greater than infinity.  He also shows that the number of real numbers is equal to the total number of these IEDSs, despite the duplications I mentioned earlier.  Thus (he says) he has proved that the number of real numbers is greater than the number of natural numbers.

•    Amateur mathematicians have for years objected that this is no more than a sleight of hand - the C number or numbers are as much a member of the target sequence as the rest, it’s just that Cantor keeps changing his numbers to be different from the ones you’ve reached in the target sequence up to that point.  But this isn’t correct.  Yes it’s a simple trick, but it works. Try it.  Cantor isn’t switching his numbers; each digit for each number he creates never changes, it just has further digits added to it.  And for any integer i greater than 1, i^n is bigger than n for any natural number n.  So at (say) the 5th term in the target sequence, there are, obviously, 5 numbers in the target sequence so far, but Cantor already has (in base 10) 9^5 5 digit C numbers outside the target sequence by his method.  Cantor has indeed given a simple and elegant proof that the real numbers can’t be put into a single sequence, either by magnitude or in any other way".  

The problem with Cantor’s diagonal proof

Danny was walking around the courtyard now. “So we are satisfied that Cantor is right that you can never get a sequence of IEDSs with no C numbers left over.  But does this prove, as Cantor believed and as is still generally accepted, that as a result the total of (i) the IEDSs in the sequence and (ii) the corresponding C numbers has to be more than infinity?  Let’s look again at how many C numbers there are outside the sequence, as determined by the diagonal proof.

•    We already have the answer to this from what we talked about earlier.  By assumption, there were infinity terms in the target sequence, as it constituted an unbounded sequence.  So In base 10, there are 9^infinity C numbers outside the sequence, and so on.  But this just gets us back to the question of how big i^infinity is.

•    Let’s start with base 2.  We only have one C number in this case.  If the first digit of the first number in the target sequence is 1, the first digit of any possible C number has to be 0, and so on - only one choice for each C number digit, so only one C number in binary.  So in binary, the number of IEDSs in the target sequence is infinity (by assumption), plus the one C number; so the total number of real numbers identified by this process is infinity+1.  And we know what that is usually: infinity.  Cantor would say infinity +1 is not equal to infinity if you cannot make a single sequence that includes both infinity and the C number, as then you can’t biject it with the natural numbers, but we reply that this is dealt with by multi-sequence bijection.

•    In base 2, further application of the diagonal argument or process to the preceding diagonal set only creates on each occasion a single further C number so all such additional C numbers are still capable of being put in a single sequence.  And anyway as we are in base 2 it is not possible to be sure that any such further C number is different from all the numbers in the target sequence; and unless it is the proof does not apply.  So the diagonal argument only generates with certainty a single C number in base 2.

•    In fact the single C number in base 2 isn’t necessarily transcendental.  We are entitled to choose the order of our target sequence numbers, so there is nothing to stop us creating a target sequence where the nth digit of each nth term is such that those digits create a recurring sequence.  As the C number has to be the mirror of the number thus created, it too will recur in that instance and so will not be transcendental, even if every number in the target sequence is transcendental.  And what if I order my sequence so that the C number is all zeros or all ones?  A partial answer to this is to require the target sequence to include every rational / algebraic number within and including the endpoints 0 and 1, as we know they can be sequenced; then at least the C number is transcendental.

•    This further step ensures that the sequence plus the C number aren’t provably countable, as they would be if they were all rational and / or algebraics.  But there is still an important point.  Here and elsewhere, Cantor has assumed that if a category of numbers, unbounded in extent, can never be placed into a sequence without omitting at least one item, then those numbers as a whole (a) can never be bijected with the natural numbers and (b) must therefore be supernumerous to infinity.  However we have seen that (b) isn’t the case, while (a) is only an assumption.  So it cannot be the case that single sequence bijection is a necessary condition to an unlimited set being equinumerous with the natural numbers.  There is accordingly no reason to object to other kinds of bijection so long as they demonstrate the necessary 1-1 matching with the natural numbers.

•    Base 2 is clearly a special case.  What about base 3? Well, Cantor has a choice of two digits at each stage for his C numbers.  So the total set of the C numbers in base 3 is equinumerous with the total in base 2 of (i) an infinite sequence of IEDSs plus (ii) 1 C number; and this total as we have just seen is infinity.  So in base 3 we have infinity terms in whatever sequence of IEDSs you choose (by construction) plus infinity +1 C numbers.  This is infinity + infinity +1 which as we have shown is infinity, as each of those two infinities can be sequenced as long as you keep them separate from each other and from the 1.   

•    We can then do the same for base 4 and each higher finite base value, without limit, by means of an infinite ascent as we described earlier.  In each base i the number of C numbers is equal to the total number of terms for base i-1, plus infinity.  As there is an infinite number of positive integers, there is an infinite number of successive finite base values. Infinity + infinity +…repeated an infinite number of times is infinity*infinity, which we have seen is infinity.  So long as each base is a finite number, which we have said earlier it has to be, then even if all these infinite sequences can never be combined, we can still biject each of them with a separate infinite subset of the natural numbers by multi-sequence bijection.  

•    Specifically, for any base i, divide the natural numbers into separate infinite subsets for the integers 0 mod i to (i-1) mod i, giving us i subsets that can be bijected with the i sequences we have derived from the diagonal set.  For every base i the diagonal set consists of a finite series of infinite sets ending with a singleton set.  So to do this precisely, we can adjust the members of two of the subsets of the natural numbers to procure that one of those subsets is reduced to a singleton set.

•    We are not suggesting that we have established the actual number of elements in the unbounded set of real numbers for any base.  All we are establishing is that the application of the diagonal proof to any set of IEDSs is never able to show that the number of elements it contains is any greater than infinity.  

•    This shows that although Cantor was right to say that there will always be real numbers outside any unbounded sequence of real numbers you care to pick, he was wrong that this means that the total number of real numbers must necessarily be more than infinity as a result.  The question so far is undecided, since the C numbers cannot be shown to include all the IEDSs that fall outside the relevant sequence.  For example, Cantor’s C number in base 2 only represents the IEDS that differs from the corresponding sequenced IEDSs at each relevant digit.  But there may also be other IEDSs that share one or more of those digits and yet also differ from every IEDS in the target sequence."

Bijection of the real numbers with the natural numbers

•    "So now we can look again at the real numbers and see if we can after all pair them 1 to 1 with the natural numbers.  We can’t sequence the real numbers themselves into a single sequence.  But this is not necessarily because there are too many of them but perhaps because they are infinite in their expression and with no least or minimum interval between them. 

•    It turns out that we can prove that the number of real numbers (assuming that they are equinumerous with the set of the IEDSs) is equinumerous with the natural numbers by indirect bijection, in three steps:

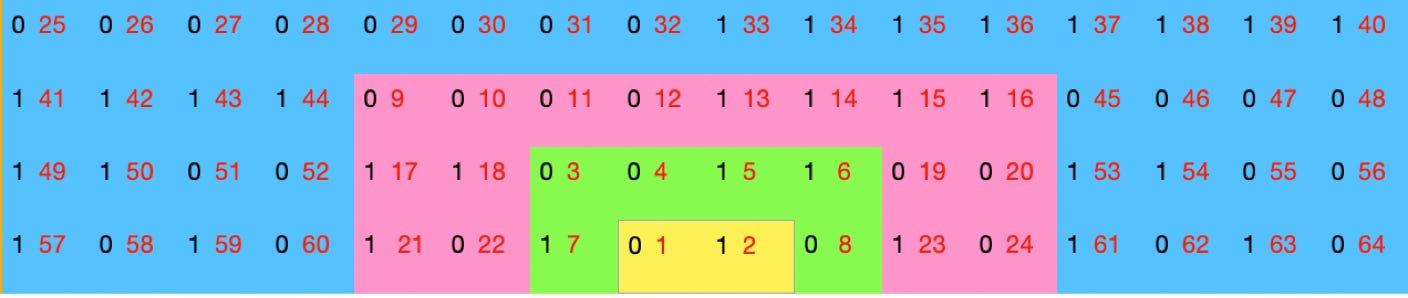
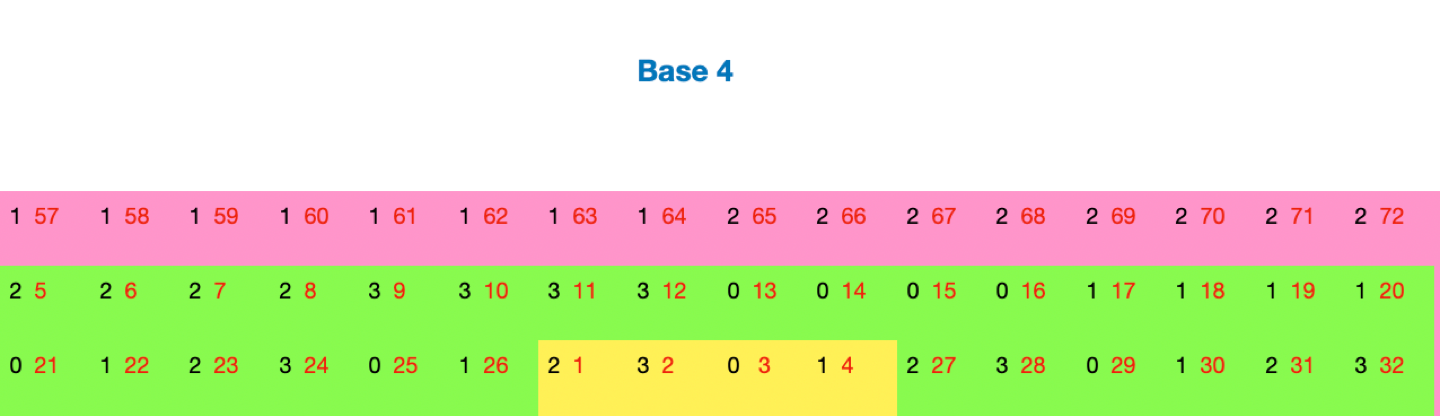
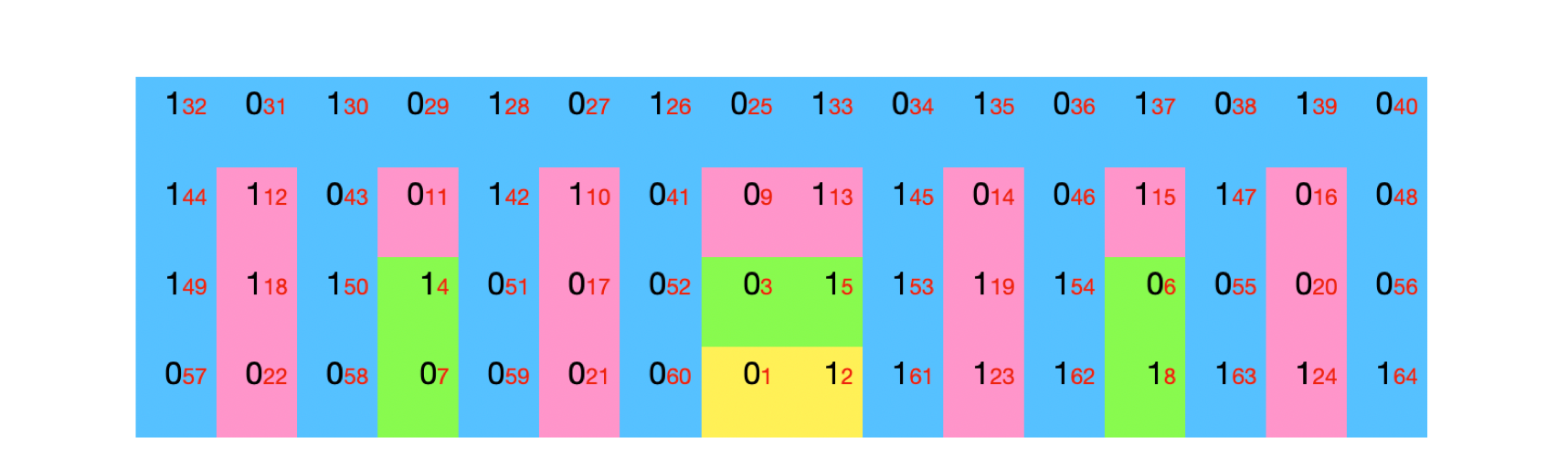
•    Step 1 We biject the individual digits of every one of the IEDSs with the natural numbers.  We use the previous idea of successive sweeps, one sweep for each additional digit of the IEDSs.  In base 2, there are two choices for each digit in sweep 1: 0 and 1 are the only choices, so they are natural numbers 1 and 2.  Sweep 2: we have 0 and 1 as the choices for the second digit for each of the two numbers, which we allocate to 3,4,5 and 6, and then we need to add another 0 and 1 as the first digits of the two new numbers we have created, allocating 7 and 8 to them.  Then successive sweeps s(3), s(4) etc add 2^s digits as the new row and you back fill the digits for the 2^s/2 new numbers you have thereby created.  At every sweep s(n) the total number of natural numbers used down to that point is 2^s(n)*s(n). Once again, a picture proved to be worth a thousand words.

•    The process is the same for higher bases.

‍  

‍ 

•  Like the set of the natural numbers and the infinity*infinity grid, we have an unbounded set of elements, this time unbounded in 2 dimensions and 3 directions.  But every single element of that set can be uniquely identified by a pair of finite x,y co-ordinates in the Cartesian plane and thus allocated a unique and finite natural number.

•    Note that using the sweep pattern in the diagram shown, we can reverse the 0s and 1s in any new row to avoid all the IEDSs generated down to that point recurring and thus becoming rational at a certain point.  This is not strictly necessary for the proof, as the elements of all the  irrational IEDSs were included in the total set, but it changes their distribution. 

•    Or, better, we can visualise the digits as spreading out like a fan, which also more closely reflects the way we naturally think of the IEDSs being generated - in base 2, two choices for the first digit, four for the second etc". "It’s a bit harder to do this in a spreadsheet", said Danny apologetically, handing me a diagram. 

‍  

‍  

‍    

•    Step 2 "So we have now bijected a set whose elements are the digits of every single possible IEDS (including therefore the digits of every single real number) (set A) with the set of the natural numbers.  Next we take a subset of set A which contains each of the first digits of each IEDS (set B).  Set B comprises the first row of our table in Step 1.  As a result we don’t need the axion of choice, in case you were wondering." I wasn’t.  "We give the elements of set B the same natural numbers as they have in set A.  We can sequence the elements of set B, even though we cannot sequence the IEDSs they correspond to, and we can also say that they constitute a proper subset of set A (ie set A contains all the elements of set B and one or more other elements), and that as a result the elements of set B cannot be greater in number than the elements of set A and so cannot be greater than infinity in number.  

•    Note that we can calculate the exact natural number allocated to each element of set B, and that this does not vary if we alter the distribution of 0s and 1s in any new row.  The formula in base 2 is 2^n for the total elements in the first row where n is the number of digits in the IEDSs down to that point, giving 2^infinity first row digits for IEDSs with infinite digits.  The procedure for the natural numbers added to the first row elements for each new n after n=1 is that we add 2^(n-1) new natural numbers, numbering back from 2^(n)*(n).  So after 4 digits of IEDSs we have 16 elements in the first row, and we added 8 natural numbers in this sweep to that row numbering back from 64.

•    A more formal way of putting it is to say that the elements of set B can be injected into set A (ie every element of set B is matched to an element of set A, and no element of set A is matched to more than one element of set B), simply by matching each element of set B having natural number n(1), n(2)… with the corresponding element in set A having that same natural number.  So set B cannot be supernumerous to set A.

•    Step 3 Finally, although we still cannot sequence the IEDSs themselves, and thus cannot match individual elements of set B with their corresponding IEDSs, we can state with certainty that the number of those IEDSs is exactly equal to the number of elements in set B, those elements being comprised of the first digit of each IEDS.  To confirm this we could for example say we allocate to each IEDS the natural number allocated in set B to the first digit of that IEDS. We can then biject the two sets. Note that we do not need to sequence either of them to do this bijection: it can be done by reference to the way each set is constructed and labelled, or what I have referred to as bijection by construction.

•    By way of confirmation, if the number of IEDSs were greater than the number of elements in set B, then there would have to exist one or more IEDSs in respect of which set B does not contain that IEDS’s first digit, as no IEDS is empty.  This would contradict our construction of set B to contain each such first digit.  So the number of IEDSs cannot be greater than the number of elements in set B.  In other words we can count the number of IEDSs even though we cannot sequence them.

We had come to a pause.  "But didn’t you prove just now," I said, "that a set of i^infinity elements can be put into a single sequence and bijected with the natural numbers?  How is that consistent with the fact that you couldn’t use single sequence bijection to prove that the real numbers and the power set of the natural numbers were equinumerous with the natural numbers?"  

"This is an example of the point we discussed earlier", Danny replied.  "It’s a consequence of the way the sets are constructed in each case, rather than the number of elements they contain.  In my initial proof we were counting elements of a set, like the natural numbers, which have a least or minimum interval between them, so that we can sequence them.  Each natural number is one unit apart from its predecessor and successor - that’s how they are formed.  The real numbers, and the members of the power set of the natural numbers, each have no least or minimum interval, and are or may be infinite in their expression, so we had to go about it differently.  But this doesn’t alter the fact that i^infinity=infinity, whether the i^infinity set can be sequenced or not."

"Fair enough", I said.  "What about the bit in Step 3 where you say you can biject the first digits of each IEDS with the corresponding IEDS itself?  You don’t pair them off 1-1 at all so can it not be argued that you are not applying any version of Hume’s Principle, and your whole proof must fail?"      

"I am still applying Hume’s Principle", Danny replied. "Bijection simply means that you can match the two sets 1-1 in both directions, with no element left out in either set and no element matched to more than one element of the other set.  There is no magic in the sequencing and diagrams people conventionally use to do this, and it would be inconsistent with the principles by which the natural numbers are generated to exclude certain forms of bijection arbitrarily.  Hume’s Principle requires me to show that every unit in one set has a unit in the other set answering to it.  It doesn’t restrict me in the way I do this; nor can there be any reason to do so.  In this case I could show by my construction of the sets that for each element of one set I had allocated it a single natural number which was also allocated to one, and only one, element of the other set, and that every element of that other set was included.  So that gives you bijection by construction; it’s a direct bijection between the two sets.  And if we look at the consequence, what we have proved is that if we take a set of subsets none of which is empty and each of which contains a sequence of digits, the number of first digits must be equal to the number of subsets, ie each such subset has one and only one first digit.  That’s hardly a controversial proposition.  

Indeed one might go further.  It was recently proposed by the maths department of a well known European university that we should look to Brahmagupta’s concept of zero for an example of a credible alternative to modern western mathematics.  Brilliant as that concept was for his time, the west’s concept of zero has moved on from Brahmagupta’s work with the benefit of several centuries of further thought.  But if you told any traditional Indian, Persian or Arab mathematician, or for that matter any exoplanetary mathematician, that 2^infinity is greater, in the cardinal sense, than infinity, then I strongly suspect they would laugh at you." 

The power set of the natural numbers

•    "Cantor applies a similar argument to show that the number of members of the power set of any infinite set is greater than the number of members in that infinite set.  His proof applies to power sets of infinite sets generally, but for convenience I will focus on its application to the power set of the natural numbers.  I am using what I understand to be the generally accepted modern version of his proof (from Wikipedia again).

•    The power set of the natural numbers has as its members the empty set plus all the possible combinations of natural numbers, starting with the integers individually, then each possible pair of integers, and each possible higher number of integers up to all the possible unlimited combinations.  The test as before is to see if we can allocate a single different natural number to each such member and vice versa (ie bijection).  So for example we could match the subset {1,2,3} to the natural number 7. 

•    Cantor then says that as we are taking all possible combinations of integers, our power set must include the set (which I will refer to as Cantor’s Set) that meets the following definition: it is the set of all natural numbers which are not included in the co-domain of any given function applied to the natural numbers.  Cantor’s followers appear to assume this set qualifies as a subset of the power set without proving it.

•    The formal expression of Cantor’s Set for the purposes of the general proof of Cantor’s Theorem is as follows: B={x∈A∣x∉(f)x}.  In English, this means that Cantor’s Set (B) is a subset of the infinite set (A, eg natural numbers) whose elements consist of every element x of the infinite set A which is not also an element of f(x), ie the particular subset of the power set to which that x corresponds because of some defined relationship f.  f is an injective relationship that matches every x to a different subset of the power set.  If the members of the power set are supernumerous to infinity, the converse will not be the case and there will be one or more subsets of the power set not matched to an x, ie f may or may not be surjective.  Cantor set out to prove there must be at least one such unmatched subset. 

•    f can be any relationship - we can simply make it the decision to match a particular natural number to a particular subset of the power set, which is what the example in Wikipedia does.  

•    We have thus divided all the subsets, or at least all those we have matched to an x, into two categories: one, where the natural number matched to a subset is also a member of that subset, and the other where it isn’t.  I’ll call the subsets in the first category, and their corresponding natural numbers, selfish, and the ones in the other category unselfish, as the Wikipedia example does.  So Cantor’s Set is the set of all unselfish numbers.

•    The proof is then simple: 

• First take every x which is not an element of its corresponding f(x).  Then B cannot be the same as any such f(x), since each such x is a member of B but cannot be a member of the f(x) that corresponds to that x.  
• Secondly, take every x that is an element of its corresponding f(x).  Then B cannot be the same as any such f(x), since B cannot contain any such x but every such f(x) contains at least one such x.

•    So, Cantor says, we have proved that B cannot correspond to any element of the infinite set A.  If the infinite set is the natural numbers, this means B cannot correspond to a natural number, so we have created a subset of the power set that can’t be matched to any natural number.

•    This proof is based on a simple paradox.  When I was at school I remember children giving each other a piece of paper.  On one side it said "The statement on the other side is true".  You turned over and it said "The statement on the other side is false".  It’s the same idea.  So was Russell’s barber paradox.  But Cantor said that because of this paradox he had created a subset of the power set which could not be allocated a number from the natural numbers.  This was very important because if at least one subset in the power set could not have an allocated natural number, there was no surjection of the natural numbers as a whole onto the subsets of the power set.  As a result there could be no bijection between (a) the natural numbers and (b) the members of the power set of natural numbers.  And as each natural number can be matched to the subset of the power set whose membership consists solely of that same number, so that every such subset is matched to no more than one natural number (injection), the number of sets in the power set must be greater than the number of natural numbers.  

•    The consensus of mathematicians accepted this proof, which became known as Cantor’s Theorem, and it is still generally accepted today.  Criticisms of it seem mostly to be based on quasi-philosophical arguments, of such vagueness that they can confidently be ignored.  Based on the proof, Cantor went on to show that the power set of the power set was bigger again, and so on in an endless stack of bigger and bigger infinities.

•    Cantor’s Theorem invites two questions: first, is it correct, and secondly, if it is correct, does it prove that the members of the power set of the natural numbers are supernumerous to the natural numbers themselves.  

•    We know that there must be an unbounded number of unselfish numbers but that there is at least one selfish number (the number allocated to the set of all members of the natural numbers).  Let's assume, without loss of generality, that all the odd natural numbers are unselfish, and none of the even ones.  The odd numbers then form an infinite subset of the natural numbers, which is Cantor’s Set.  Let us then assume that so far Cantor’s Set has no number, or if it has one we remove it.  Cantor is right that I cannot give Cantor’s Set a number which is an element of Cantor’s Set (as all those numbers are by construction allocated to other subsets) and that if I give it an even number, (let us say 2) which is not a member of Cantor’s Set, then Cantor’s Set ceases to hold all the unselfish numbers.  But that is not the same as saying I can’t give it an even number, such as 2 - I just did.  

•    It’s the same with other forms of this paradox.  Logicians say that it is impossible for Russell’s barber either to shave himself or not.  But if you go to the village and have a look, you will find that he either does or doesn’t shave himself.  The problem lies with the embedded contradiction in the proposition, not with the factual situation.  Cantor’s Set has two logically independent membership criteria: (a) that it contains all the specified members (in this case all the unselfish numbers); and (b) that it doesn’t contain anything else.  Those criteria are incompatible a priori.

•    So I now have a perfectly good subset which has an allocated number.  It it is just that it has ceased to be the subset containing all the unselfish numbers, since it doesn’t contain itself.  If we then require it to be the set of all unselfish numbers, we .have to make 2 a member of Cantor’s Set.  Which makes 2 selfish so we have to take it out again.  Thus the composition of Cantor’s Set is uncertain.  So it isn’t a member of the power set as defined, because it doesn’t consist of a particular subset of natural numbers but nor is it empty.  Indeed it could be argued that it isn’t a set of any kind.  

•    As Cantor’s Set isn’t a member of the power set, we have to take away its number, as we are only numbering members of the power set.  But this doesn’t matter since we do so only because it is not a member of the power set.  So all members of the power set still have numbers.  As soon as I take the number away, the subset’s membership becomes certain so it becomes a subset of the power set again and gets its number back, and so on.

•    So Cantor’s Set cannot have a number only to the extent that it is not a subset of the power set, and to the extent that it is a subset of the power set it is able to be allocated a number.  

•    Note that Cantor’s Set is always associated with a particular number (in this example, 2).  We can reserve that number for Cantor’s Set throughout, whether or not we formally allocate it to Cantor’s Set at any particular point pursuant to the f function.  And this reserving of the number 2 will have no impact on the question of whether or not we can allocate a natural number to each subset of the power set as we will still have an infinite number of other natural numbers.  In other words, we are dealing with the simplest form of multi-sequence bijection where we divide the natural numbers into two subsets - first, the singleton set 2 and then the set of the rest of the natural numbers, and match them all with the subsets of the power set, including the Cantor Set.  And importantly, we can do this whether we think Cantor’s Theorem is right or wrong.

•    Finally, you will have noticed that we started by assuming we can determine which sets in the power set are selfish and which are unselfish, disregarding Cantor’s Set.  This is the assumption Cantor made, but it isn’t correct, because of Cantor’s Theorem.  You cannot assume any category or list of numbers, finite or infinite, are the unselfish numbers.  If they were they would comprise Cantor’s Set, and we would have all the problems we’ve just described.  All we can do is take any finite or infinite list or set of unselfish numbers; then our proof shows that that set cannot be the set of all unselfish numbers.  Cantor’s Set doesn’t exist at all, let alone constitute a member of the power set of the natural numbers, as Cantor also assumed.               

•    So we are still left with the more important question of the number of members of the power set.  This number is well known; as I explained, it is considered to be not infinity^infinity, but 2^infinity, since position, by generally accepted principles, is irrelevant.  Each element (in our case a natural number) is either in, or not in, any given subset in the power set.  So that’s two choices per number for an infinity of numbers giving 2^infinity permutations, or subsets.  Western mathematicians generally accept this - indeed I believe power sets of this kind are known as 2^N sets where N refers to the number of natural numbers.   But you get to 2^N sets, ie 2^infinity sets, without Cantor’s Set.  If Cantor’s Set is an additional subset to the others, as Cantor claimed, which cannot be included in a sequence with them, you would have 2^N + 1 sets - not as punchy.  Indeed you can construct equivalent sets to Cantor’s Set by looking not at whether the number (x) allocated to the set is in the set as well to decide selfishness, but at whether some function of that number, eg x+1, x*2 etc is to be found in the set.  You end up with an unbounded number of different Cantor Sets.  If you think that as Cantor believed they are all subsets of the power set, there would be not 2^infinity, but 3^infinity subsets in the power set - each natural number can be in, out or a flip flop between in and out.  

•    But whether the Cantor Sets are members of the power set or not, we can use indirect bijection to show that every element (ie natural number) in every subset of the power set can be matched to a single natural number, and vice versa.  We use a 2^infinity or 3^infinity grid to represent every element of every subset.  Assuming 2^infinity, we include each successive natural number in our grid in two forms: one colour (eg green) if it is in the corresponding subset and another colour (eg red) if it is not, allocating to each natural number n(1), n(2)…. the row for which y=n.  Or if you prefer we can use a 1 for a natural number that is in its subset and 0 if it is not.  The grid is then the same as our grid for Cantor’s diagonal proof.  Having shown that the individual members of each subset of the power set are countable, we can show that the number of those subsets is also countable, as we did with the real numbers.  That analysis will then apply to the power set of the power set, and any other power set of an infinite set.  All those power sets have an infinite number of members, no more, no less.

•    If we want to include the flip flop numbers generated by Cantor’s Theorem as separate elements, the process is the same but with three numbers or colours instead of two.

•    Even if position in the set mattered so that we had infinity^infinity members of the power set, we could use the version of the indirect bijection method we described earlier, based on a hypercube of unlimited dimensions and extension.  Again we are bijecting the individual elements of the subsets of the power set with the natural numbers because we cannot biject the subsets themselves because of their infinite extension and the absence of a least interval.

•    For ease of visualisation, we can also prove this result by our other form of indirect bijection, by (i) taking a Cartesian grid of the integers constructed as before; (ii) substituting successive primes for the successive integers; (iii) multiplying every prime at x=1 by every prime at x=2, and so on for every value of x, and (iv) to deal with the fact that at x=infinity all our values equal infinity, put a fractional separator at the beginning of each number that results; so we have the IEDSs which we have already dealt with". 

I tried a question.  "You have shown that the number of subsets in the power set of the natural numbers, ignoring Cantor’s Set, has to be 2^N, and that that is also the number of real numbers in binary.  So if Cantor’s Set was also a subset of the power set but not able to be sequenced with the other subsets, as Cantor argues, that would on Cantor’s analysis make the number of members of the power set bigger than 2^N and so bigger than the number of reals.  And yet western mathematicians who accept Cantor's argument say that the number of the reals is the same as the number of members of the power set of the natural numbers, including Cantor’s Set.  How can these propositions be reconciled?"  "I don’t know" said Danny, "but logicians say you can prove anything if you start with a false premise."

Ordinals

'Two and two are four.'
'Sometimes, Winston. Sometimes they are five. Sometimes they are three. Sometimes they are all of them at once. You must try harder. It is not easy to become sane.'

•  "At this point we need to consider ordinal numbers and their possible effect on our analysis.  Ordinals as we now know them were another creation of Cantor's, apparently because he was working on a repeating calculation using ever larger numbers, and he would get a better result if he could go beyond infinity; rather like the schoolboy in the playground, who "bags" something infinity and one times to beat his friend’s infinity times.  

•    You will read that cardinals count the number of objects in a group of some kind, while ordinals look at the position or rank of numbers in a sequence - hence the name.  This is only partly true; ordinals are still counting numbers in some respects, but as ordinals they only count one thing, the number of ordinals preceding a given ordinal in the sequence of ordinals.  This sequence is arranged by magnitude, and of course magnitude itself is a cardinal concept.  

•    Cardinals are defined by the number of things they count, and their value is unchanged however they are arranged.  As we said earlier, they are like pool balls with a number on them - you can put the balls in a bag, shake them up, and the numbers don’t change.  Ordinals as Cantor conceived of them are like the queue for the late Queen's funeral in London.  Each ordinal has a place in the queue, starting at the front with number 0.  You can only join the queue at the back (higher numbers) and you take your number when you join from your position in the queue, which can’t change.  Once the queue becomes endless you cannot join the end because there is no end, and you have to start a new queue - like the queue to join the queue, in the case of the funeral.  

•    We talked earlier about the property of the natural numbers which means 7 is the 7th natural number etc (assuming you start from 1 not 0). In the same way the ordinal 7 is preceded by 7 ordinals (starting at 0) so its ordinal value is 7. The difference is that infinity (or ω), which is preceded by an infinite number of finite ordinals (the natural numbers including 0) becomes more like another fixed number, like 1,000, and you go on from there to ω+1, ω+2….It is referred to as a 'limit" rather than a number, since you do not reach it by adding 1 to the immediately previous ordinal - indeed there is no immediately previous ordinal.

•    It is the sequential characteristic of ordinals that is said to require a new ω to be started as soon as the preceding sequence has become unbounded, because at that point it becomes impossible to add to the preceding sequence as there is no last member.  But this is not a consequence of the members being ordinals.  The same would apply if they were cardinals.  The reason is that for these sets, the membership of the set, as defined, is complete.  A set of the natural numbers can only consist of one example of each number.  So such a set, although infinite, cannot be added to at all, whether its members are ordinals, cardinals or anything else.  You can only add members to it if you change the rule for its membership, which turns it into a different set.

•    Other sets are incomplete and can be added to indefinitely.  The members are fungible, like identical honey pots, and when sequenced the ordinal values are dictated by the position in the sequence, not vice versa.  If new members are added and the position of an existing member changes, so does its ordinal value.  If Kanga gives Pooh two more pots and he puts them between the 3rd and 4th pots, the 4th becomes the 6th.

•    Whether you treat ordinals as (a) the number of all preceding ordinals or (b) the immediately previous ordinal +1, you have to make an additional assumption to deal with (respectively) ω+1 or ω.  You are entitled to make these assumptions, but they are arbitrary.  Mathematicians had to restore an element of cardinality into the ordinals, by having each ordinal represent the number of its predecessor ordinals, which allowed them to incorporate infinity.  But having defined infinity as the number of preceding ordinals, we have to abandon this concept for ω+1, as adding 1 to infinity is still infinity, quantitively speaking.

•    Describing ordinals as being equal to the number of preceding ordinals including 0 does not reflect normal usage.  Pooh regarded his 6th honey pot as the 6th because there were 6 including that pot in his row of pots.  He did not say to himself that there were 6 pots preceding it, one of which was the space to the left of the first pot where there was no pot.  We can say with confidence that he would not have regarded an absence of pots as equivalent to a pot.  And similarly you need considerable mental agility to persuade yourself that there can be such a concept as the infinitieth item in a sequence.  So ordinals as understood by mathematicians are not the same as ordinals as generally understood by the rest of humanity.  Mathematical ordinals are, or at least set out to be, a separate and self contained system of numbers, while normal ordinals are descriptive or adjectival terms derived from the natural numbers (first, second, third…).

•    Pooh’s pots also remind us that ordinals in normal usage can be determined by the number of preceding items in any set, not just other ordinals.  The requirement is simply that the objects to be counted are sequenced in some way, either by a characteristic such as magnitude, or arbitrarily, like Pooh’s pots, so that we can match them to the successive ordinals.  

•    The concept of comparing the size of a set of numbers with another set remains. But it is not called bijection this time.  Instead it is described as establishing the order type of the two series, and determining if one is isomorphic to the other.  For example 2*ω+4 is said to have the same order type as the even ordinals up to 2*ω+8 since in each case there are two series of ω and then 4 finite ordinals.  This exercise, like bijecting cardinals, involves a 1 to 1 matching to see if the number of elements is the same.  It seems counter intuitive however to talk about a set of ordinals whose members consist of anything other than a set or subset derived from the successive natural numbers starting at 0 or 1.  The ordinal is meant to be defined by its place in the sequence, or the number of its predecessors. By contrast in a set of the even natural numbers, 6 is the third number not the sixth.  And successive members of the set are generated by adding 2 not 1 to the predecessor member.

•    Setting aside for the moment the possible difficulties we have touched on, the rules for ordinals, so far as relevant for our present purposes, can therefore be summarised like this:

‍    (i)    Finite numbers are the same as cardinals but you only use natural numbers, including 0.  

‍    (ii)    Because you include 0, and because each ω multiple is the next number after its corresponding infinite series, each ordinal can (with certain qualifications) be regarded as equivalent to the number or quantity of all preceding ordinals.  It can also, again with qualifications, be regarded as the immediately preceding ordinal +1.

‍    (iii)    As soon as you get to an unlimited or infinite sequence of ordinals, you start a new sequence.  Think of them as the columns for x=1, x=2 etc in the Cartesian plane, each with an unbounded number of values along the y axis.  People talk about the next ω sequence coming after the "end" of the previous one, but as each ω sequence has no end it is easier to think of starting each new sequence apart from the first from a multiple of ω each time, leaving the previous sequence unbounded.

‍    (iv)    As with cardinals, if you start with either 0 or any natural number, adding ω to it gives you ω.  So 0+ω, 100+ω etc all = ω.

‍    (v)    However ω+8 is bigger than ω and so bigger than 8+ω, because once you get to ω you start a new sequence equivalent to the previous one.

‍    (vi)    As we discussed earlier with infinity, you can then have 2*ω, 2^ω, ω*ω etc, but this time each of those numbers is "bigger" that the preceding one just as they would be if you were counting thousands or millions.

‍    (vii)    The system of ordinals is effectively self contained because of the way they are generated.  Ordinals are only used to count ordinals.  Cardinals can count anything including ordinals.

•    Two points follow from these characteristics that are relevant to our discussion.

‍    (i)    Because finite numbers are the same in ordinals and cardinals, and both infinity and ω are equal to the number of natural numbers, 2^infinity in cardinals is the same calculation as 2^ω in ordinals.  In each case it gives you 2*2*2*2….or 2+4+8….which is infinity or ω.  Mathematicians recognise this obvious fact with ordinals.  But since they have to believe 2^infinity in cardinals is greater than infinity, they say the calculation is "of course" quite different in the two systems.  It isn’t.  It’s the same.  It has to be.  More generally, because each ordinal is generated from the sub-sequence of individual ordinals that precedes it, starting at 0, mathematicians have to accept that all ordinals which are a multiple or exponent of ω or ε (ε is like ω but bigger) are part of a single sequence, and so their members are countable for the purposes of determining the cardinal number of ordinals in the relevant sub-sequence that precedes them, ie there are never more than infinity of them.  

So this is another problem for the idea that 2^infinity in cardinals is bigger than infinity.  If it was, the same would have to apply with ordinals, and it doesn’t.

‍    (ii)    Mathematicians say that beyond the infinite but countable sequences of multiples and powers of ω, and its successor sequences, still countable, of multiples and powers of ε, there is a larger ordinal which corresponds to an unsequenceable and uncountable number of preceding ordinals, called ω1, and then a series of greater uncountable ωs thereafter.  But this can’t be right.  So long as you create ordinals step by step, either by adding 1 or by multiplying or exponentiating ω or ε or any successor to ε, or by taking the number of all preceding ordinals, you can never get to an uncountably large set of them.  This would be the case even if we could identify numbers cardinally greater than infinity, such as the number of real numbers, or of the members of a power set of an infinite set, as no such set could be put into a sequence and therefore there can be no set of ordinals corresponding to such a set.  And by our analysis those numbers are not cardinally greater than infinity in any case.  ω1 is thus inconsistent with the principles of the ordinal system, and all known sets of ordinal and cardinal numbers, as currently defined, have only an infinite number of members.

The perceived need for an ordinal that is bigger than the countable ordinals, or bigger than all the ordinals, may partly be a consequence of the system adopted to create each successive ordinal.  At every step, the ordinal created is not included in the sub-sequence of preceding ordinals.  So the system can only work if you are dealing with a proper sub-sequence of the set or series of ordinals as a whole (ie a sub-sequence that doesn’t include every member of the set as a whole).  Applying it to the sequence of ordinals in its entirety immediately throws up a contradiction - if it’s the sequence in its entirety how can there be another ordinal outside it? 

You can avoid this problem by adopting an alternative, and perhaps more natural rule for generating ordinals: instead of starting at 0, start at 1.  Like Pooh’s pots.  Then each new ordinal is the total number of ordinals in the sub-sequence including the new one itself, not excluding it.  The sequence of ordinals created by both the generally accepted rule and the alternative rule is the same in all respects except that our new version has no 0.  Each ω becomes the limit or last member of the unbounded sequence that precedes it rather than the start of the next sequence, though its position in the sequence is the same in each case.  Then the countable ordinal that corresponds to the set of all ordinals is the same as the number of ordinals in that set, and so can be an element of that set, ie countable.  This change works because the number of ordinals up to and including ω is the same as the number up to but excluding ω.  ω is preceded by an unbounded number of ordinals but each of them is finite, making ω the first infinite ordinal.  

There are other arguments that prove that the set of all countable ordinals is uncountable, such as Hartogs’s Theorem, but I believe they also depend on the proposition that an ordinal cannot be a member of itself (when considering ordinals as sets).  If so this is an assumption rather than a necessity.

So the system of ordinals, properly considered, does not require us to accept that there can be numbers bigger (in the cardinal sense) than infinity.

Counting

Manco:  No, old man. Thought I was having trouble with my adding.  It’s all right now. 

So next let's see if we can arrive at a clearer understanding of numbers, preferably without recourse to the Greek and Hebrew alphabets, in the light of our analysis.  

‍    (i)    The natural numbers are individually finite but as a set they extend to infinity.  It is not possible to extend an infinite sequence "beyond" infinity, as there is no terminal point.  No matter what numbers you add to infinity you still get infinity.  This is the case whether you consider the natural numbers in their ordinal or cardinal aspect.

‍    (ii)    We saw earlier that it is simple to define a multiplicity of infinite sets, whether of numbers or anything else.  A single infinite set S can be divided into an unlimited number of infinite subsets ss…, and a set of two or more infinite subsets ss… can be combined into a single new set S, with new membership criteria if the subsets are complete (eg odd and even numbers combine to give the natural numbers).  The number of members in the set S is the same as the number in each subset s, and the total number of members in all the sets ss… is the same as the number of members in S.  So if we want to extend the natural numbers beyond infinity, we generate two or more infinite subsets ss… and then count those subsets instead of counting their individual members, while keeping the subsets separate.  This gives us 2 infinities, or any greater number you please of infinities.  The concept applies to all numbers or other things that can be conceived of as the members of a single infinite set.  It’s not something we have to do - we could limit our number system to the natural numbers - but it is something we can do in a way that extends the natural numbers while maintaining consistency.

‍    (iii)    The generation of numbers based on separate infinite sets is not dependent on the sequential character of ordinals. Still less is it the inevitable result of our definition of ordinal numbers, whether based on succession or on counting predecessor numbers.  As we explained earlier, you have to introduce at least one arbitrary assumption to arrive at transfinite ordinal numbers, however you generate your ordinals.  

‍    (iv)    Ordinals and cardinals represent two aspects of these numbers, both finite and transfinite.  The numbers are quantitatively generated.  Their cardinal aspect signifies the number of members in any set or subset (quantity) and the ordinal aspect signifies the last member of that set or subset when sequenced (order or rank).  So there are 11 even numbers from 10 to 30.  30 is the 11th when sequenced by magnitude or by the number of their different prime factors.  But when placed in alphabetical order, 30 is the fifth because it is the last member of the subset {18, 14, 16, 10, 30}.

‍    (v)    For every ordinal value there has to be a corresponding cardinal value, because the ordinal value is derived from the corresponding cardinal.  So if you want your system to include transfinite values you have to have transfinite cardinals to correspond to the transfinite ordinals.  All those numbers are generated in the same ways whether you regard them as ordinals or cardinals or both, the only distinction being between finite and transfinite numbers.  Transfinite numbers consist of natural, ie finite numbers coupled with one or more infinite sets.  All numbers, whether considered as ordinals or cardinals can refer to any kind of members of any kind of set, from numbers to honey pots.  

‍    (vi)    Cantor and his successors had to treat ordinals and cardinals as mutually independent for three main reasons: (a) to remove or at least minimise the quantitative attributes of their transfinite ordinals; (b) to allow for the fact that their transfinite ordinals were generated differently from their transfinite cardinals; and (c) to get round the problem they had with 2^infinity.  The last two don’t apply in our analysis, and in the case of the first, we are open about the fact that our transfinite numbers are no greater than infinity in its conventional cardinal sense.

‍    (vii)    It might seem that infinities and numbers including an infinite element are therefore not proper numbers, but more like sums; 2 infinities looks like a sum requiring you to add infinity + infinity.  If you do this in the conventional way, by combining the two sets into a single set and counting its members, you get infinity.  However most of our natural numbers are also expressed as sums; they just use position to imply exponentiation and addition.  133 means 1*10^2+3*10^1+3*10^0.  Transfinite ordinals as currently defined by mathematicians can also be regarded as sums in this sense, and the "answer" to every transfinite ordinal, regarded as a sum, is infinity.  As we saw earlier, arithmetic sums of this kind are synonyms for the corresponding answer, so they can legitimately be regarded as numbers.  It’s just that all sums with an infinite component are synonyms for the same answer - infinity.

‍    (viii) Because we don’t have to distinguish between ordinals and cardinals, even at transfinite values, we can dispense with Greek and Hebrew letters or any other distinguishing feature.  For all mathematical purposes we only need to deal with numbers, without specifying whether they are ordinal or cardinal.  And we always know whether or not we are adopting the convention of counting infinite sets to arrive at transfinite numbers, as we only get transfinite values if we do adopt it.  So we can write transfinite numbers, which arise when we are counting infinite sets, in a form such as 123∣456.789, where the digits to the left of the vertical are the infinities, and we can (with a bit of ingenuity) add, subtract etc the combined numbers accordingly, without labelling the infinities as ordinal or cardinal.  

‍    (ix)    The finite and infinite components both count things (units and infinite sets respectively).  The infinite component is never so far as we know cardinally greater than infinity in the conventional sense of counting units. Infinity and multiples of infinity cannot have an ordinal aspect, because they can never represent the last number in a sequence of numbers.  There is no reason for infinity to be included as a member of any infinite set of numbers, whether it is a single set or one of two or more sets that we are counting together to form a single transfinite number.  Excluding infinity means that all members of such sets have both ordinal and cardinal aspects and can be regarded simply as numbers,  and also means that each of the infinite sets we count has the same membership.  However the infinite component of a transfinite number with 0 as its finite component still has an ordinal aspect because the number of infinite sets making up the infinite component has an ordinal aspect.

‍    (x)    Once our transfinite numbers reach an infinite number of infinite sets, you cannot increase that number of infinite sets directly as it will always be infinity however many infinite sets you add.  So you repeat the process by treating your infinite number of infinite sets as a single set and then generate further infinite sets of infinite sets.  Then when you get to an infinite number of these sets you go on to the next level and repeat, and so on ad, as it were, infinitum.

So I’m not suggesting ordinals as currently defined are wrong.  Rather, they seem in their currently accepted form to be an unnecessarily contrived way of getting to the result - a succession of numbers with values beyond infinity -  that Cantor pursued so doggedly to satisfy his desire for a mathematical Tower of Babel; a case of reason serving as the handmaiden of faith.  

Cantor and his successors are like the villagers in Charles Lamb’s A Dissertation Upon Roast Pig, who thought they had to set their houses on fire every time they wanted a Sunday roast.  I am suggesting they try an oven".  

𝗤 = ℝ = 𝗣(𝗡)

"Before we go, here’s a simple identity, or quasi identity, which summarises and confirms what we’ve discussed so far.

•    We know that the number of real numbers in binary is 2^N, or 2^infinity, since we have an unlimited sequence of digits for each number in a single sequence, with two choices for each digit.  As we saw, we do not need to adjust for duplicate numbers.

•    We also know that the number of members of the power set of the natural numbers, ignoring Cantor’s set and similar sets with no identifiable memberships, is 2^infinity, as for each subset of the power set a natural number is either in or out.  And changing the location of a number in that subset does not create a new subset.

•    We saw that 2^infinity is 2*2*2*2…which is 2+2^1+2^2+2^3…, or 2+2+4+8+16….  We can generalise this for i, being any positive integer, to say i^infinity is i+(i^1*(i-1))+(i^2*(i-1))… eg 5^infinity is 5+5*4+25*4+125*4…

•    Now take the rational numbers in binary positional notation.  Between and excluding 0 and 1, and excluding terminal zeros which refer to either 0 itself or a repetition of a previous number ending in 1, we have, taking digits after the fractional separator, one single digit number: 0.1; two 2 digit numbers, 0.01 and 0.11; four 3 digit numbers, and so on.  This gives 1+2+4+8…  And as this sequence includes only numbers with a finite number of digits, then although there are infinitely many such finite numbers, the sequence excludes all the recurring numbers.  There will always be at least one recurring number in binary or any other base, because for any integer base i where i>1, i is always co-prime with i+1.   

•    The sequence for non-recurring rational numbers can be generalised to (i-1)+(i^1*(i-1))+(i^2*(i-1))…

•    So we have the following sequences:

Powers of base 2

𝗤      1+2+4+8…

ℝ       2+2+4+8…

𝗣(𝗡)  2+2+4+8…

Powers of all higher integer bases i

𝗤      (i-1)+(i^1*(i-1))+(i^2*(i-1))…

ℝ       i+ (i^1*(i-1)+(i^2*(i-1))…

𝗣(𝗡)  not applicable

So we can see that in every case the sequence A (which counts non-recurring rationals) is identical to the sequence B (which counts the reals and, where applicable, the members of the power set of the naturals), save that the first term of A is always smaller by 1 than the first term of the corresponding version of B.  Therefore once you add at least one recurring fraction to A, B can never be supernumerous to A.  You can of course derive the same sequences from the set of the natural numbers or any other infinite set, but the fact that A and B each generate the same values at each successive step after the first, and each have the same (infinite) number of steps, surely removes any argument that the two infinities are quantitively different".

Conclusion

Combien de choses nous servoyent hier d’articles de foy, qui nous sont fables aujourd’huy?

Around us, the birds in the trees were now wide awake.  Unlike me; I had been dozing on and off for a while, though Danny didn’t seem to take this amiss.  “So what have we learned?" Danny asked, I hoped rhetorically.  

"A number of things:

•    Cantor’s Theorem is ingenious but wrong.  And even if it were correct, it would not prove that the real numbers are supernumerous to the natural numbers;

•    Cantor’s two real number proofs achieve what Cantor originally claimed for each of them, but neither of them proves that the real numbers are supernumerous to the natural numbers; 

•    There is currently nothing to suggest that there is any cardinal number bigger than infinity, and there are grounds for considering that there can be no such cardinal number;

•    The continuum hypothesis is correct, in the sense that there is no cardinal number between the number of natural numbers and the number of real numbers (because they are equal);

•    The set of real numbers and the power set of the natural numbers are still equinumerous;

•    i^infinity has ceased to be anomalously big, cardinally speaking;

•    We no longer have to find room for the proposition that a proper subset can be supernumerous to the set of which it forms part;

•    We can resolve an anomalous difference between cardinal and ordinal numbers, and we can give a clearer and more coherent description of numbers and their ordinal and cardinal aspects;

•    Cantor’s Paradox is not simply an anomaly or paradox, but supports the argument that Cantor’s Theorem is wrong.  What we might call Cantor’s Irony;

•    And most importantly, we have discovered a new way of determining how many angels you can get on a pinhead, though only if they are singing not dancing."

"So", I mused, "I suppose that just leaves the question of whether it can be proved that there are no numbers cardinally greater than infinity?" 

Danny said nothing, but handed me a final piece of paper.  I put it in my pocket to read some other time.

Everybody said: "Lord! How splendid the Emperor's new clothes are. What a lovely train he has to his coat! What a beautiful fit it is!" Nobody wanted to be detected seeing nothing: that would mean that he was no good at his job, or that he was very stupid.

"But he hasn't got anything on!" said a little child. 

© danny gumm.   Copyrights in Toy Story 3, 1984, The House at Pooh Corner and For a Few Dollars More acknowledged.  Other quoted passages public domain.  

Danny danny.l.gumm@icloud.com